◆大阪府<数学>講評(開成教育グループ 提供)
<数学C>
昨年度より易化。例年に比べても比較的取り組みやすい部類に入る。
過去問練習を通じて、今までの傾向を把握しつつ練習できている生徒にとっては、見通しの立てやすい問題が多かった。大問1は小問集合と関数、大問2は平面図形、大問3は空間図形と例年通りの配列であった。大問数3題、小問数17題は昨年と同じである。
記述については例年通り2問。相似の証明と関数での求め方記述と、これまでの内容を踏襲している。例年に比べ、複雑な計算・処理を要する問題がなく、問題の解法を見抜けた生徒は高得点が期待できる。ただし、大阪府のこれまでの傾向と同様、図形の問題設定には工夫を凝らして作成され、問題集では多く見かけないタイプのため、ポイントを見抜けたかどうかで差がつくものと考えられる。文理学科設置校の場合、90点満点中7割を確保したい問題であるが、ボーダーラインは6割前後であると推測される。

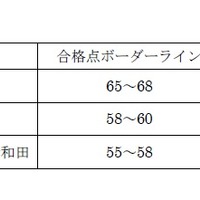
画像:数学Cの予想合格点(90点満点)※TOP10高受験者のみ
<数学B>
昨年度より易化。例年に比べても比較的取り組みやすい部類に入る。大問2の1次関数も例年通り規則性からの出題に戻った。図形問題においても相似および三平方の定理を利用していくことで解決できる。過去問演習を通じて練習できている生徒にとっては、よく見たような形式が多く、取り組みやすい問題であったといえる。大問1は小問集合、大問2は関数、大問3は平面図形、大問4は空間図形と例年通りの配列であった。大問数4題は昨年と同様、小問数22題は昨年より1題増加した。
記述については関数の記述問題がなくなり、昨年度の3題から、今年は1次関数での求め方と、相似の証明の2題に減少している。B問題を採択している高校のボーダーラインは90点満点中50点前後になるものと考えられる。
---
このレポートは平成30年3月13日(火)に開成教育グループが作成したもの。
協力:開成教育グループ