公式の暗記と異なり、受験直前の詰め込みでは対応しきれないのが、図形問題の特徴だ。空間認識力だけでなく、さまざまな条件を考慮し、いくつも筋道を考えて、その中からもっとも良いと思うことを選択する力。そのスキルを測り、鍛えることは思いのほか難しい。
本企画では、そのきっかけとして「算数ラボ図形 空間認識力のトレーニング」から、思考力と空間認識力を養う問題を紹介する。駒込高等学校や郁文館高等学校の推薦入試において、一定の級以上の合格実績で優遇措置が取られる「算数・数学思考力検定」のサポート教材にもなっている問題集だ。東京学芸大学名誉教授の杉山吉茂氏、元早稲田大学教育学部・教授で数学教育を専門とする渡邊公夫氏らが監修。
今後もますます増えると予想される、考えるプロセスや思考力が問われる入試。図形問題で、いざトレーニング開始。
(問題提供:iML国際算数・数学能力検定協会)
「算数ラボ 図形空間認識力のトレーニング6級」より
問題:形のはっきりしない図形の面積
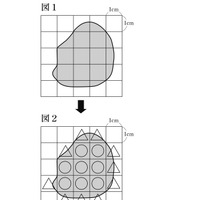
図1のように、形のはっきりしない図形の面積の求め方を考えます。
図2のように、1目もり1cmの方眼のマス目が全部図形の中に入っているところには○印、一部だけ入っているところには△印をかき入れます。それぞれの個数を数えると、○印が8個、△印が10個あります。
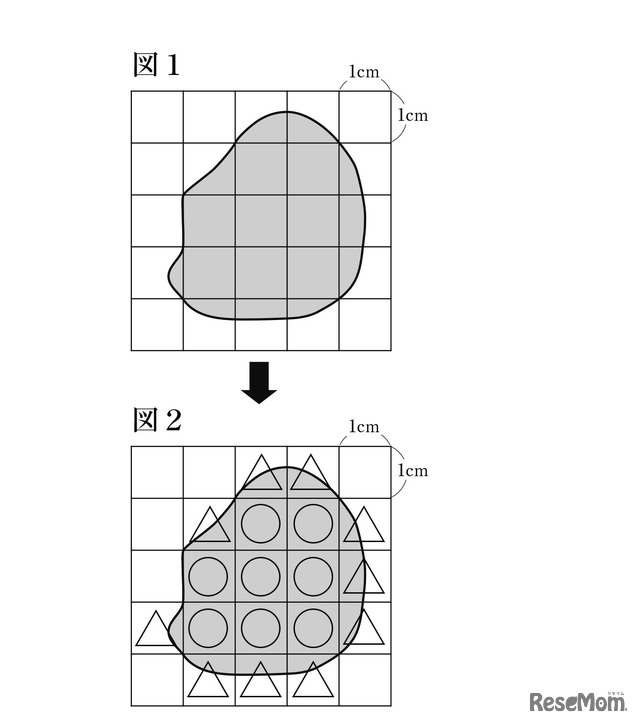
○印のところは、1辺が1cmの正方形なので、1個分の面積は1㎠です。△印のところは、1個ずつの面積はわからないので、どれも○印の半分の0.5㎠と考えます。
すると、だいたいの面積は、
1×8+0.5×10=13(㎠)
とわかります。
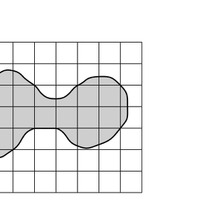
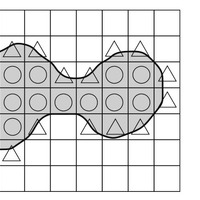
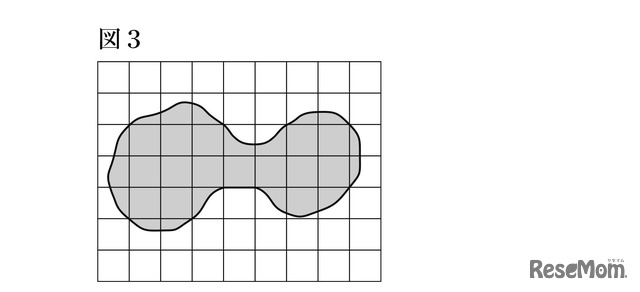
これと同じように考えて、下の図3の図形のだいたいの面積を求めなさい。 ただし、1目もりが1cmの方眼とします。
解答は次のページへ。